Puzzle events
Some puzzles I write are for specific events. Many of them are logic puzzle contests; in other cases, they are part of a single hunt puzzle.
In this archive, puzzles are filed under their respective genres regardless of what event they appear in. Unfortunately, this means puzzles of a single event are spread out, even though some people think they should be together.
This section contains puzzle events for which I've written logic puzzles. Each event also has all the logic puzzles gathered together. The events are ordered chronologically.
- BM Puzzle Competitions ()
- Deception ()
- First April Sprint Test ()
- Polyglot ()
- NEW, HUGE, AND CHALLENGING! ()
- Puzzle Marathon 2016 ()
- The Great Abacus ()
- Unusual and Strange Puzzle Collection ()
- 18th 24-Hour Puzzle Championship ()
- Allied Occupation ()
- Something is Off ()
- 19th 24-Hour Puzzle Championship ()
- We are Puzzlers Club ()
- Typed Logic ()
- 25 Years ()
- Indian Puzzle Championship ()
- RED SUS ()
- 20th 24-Hour Puzzle Championship ()
- 21st 24-Hour Puzzle Championship ()
- Serbian Puzzle Championship 2024 ()
- 22nd 24-Hour Puzzle Championship ()
Where to find events written by me
There are a few places where I consistently write for. Most of the events fall under one of these.
24-Hour Puzzle Championship
24-Hour Puzzle Championship (24HPC) is an annual competition that takes place offline, in Budapest, Hungary. You have to solve logic puzzles all day long, throughout a full 24-hour period with only a few breaks. In total, you are doing 13 rounds, each one lasting 100 minutes. (There are 14 rounds prepared, with one rotating round; if someone writes for a round, they get the rotating round when it would be their set for everyone else.)
I started writing for 24HPC in 2018. Well, "I" might not be the right word. I organized rounds together with Puzzlers Club. We would decide on a theme, and people would write puzzles for the theme. We have written rounds for 24HPC since 2018.
If you're interested in past puzzles and results, I have a 24HPC archive as linked above. Thanks to various contributors, I have complete archives from 2007 onward, plus most of 2006 (some authors didn't release their puzzles from that year) and a smattering of 2003–2005.
Unfortunately, 24HPC has an extremely poor track record of maintaining an online presence. Events were broadcast either on the UKPA forums or as Facebook events, with no website of them or anything. That's part of why I was inspired to collect what I could find into my archive.
Logic Masters India
Logic Masters India (LMI) is the main place that organizes activities about logic puzzles in India. It also runs national championships to select people to go to the World Sudoku & Puzzle Championships.
But LMI also has a large online component. It has infrastructure to run contests online, where you can log in during the contest period (typically over a weekend) and start a contest any time that is suitable for you. Many people have written contests for LMI, including myself.
The first LMI contest I took part of was Melon's Puzzle Zoo, by Palmer Mebane (MellowMelon) in February 2011. I believe this was very soon after I was introduced to logic puzzles in general, including finding Palmer's old blog Melon's Puzzles. On retrospect, the test was pretty tough as my first one, but I'm happy I took part in it, and it drove me to keep competing and do better in general.
The first contest I wrote was Deception in May 2013, and I've written several more contests since then, some of them with Puzzlers Club.
Puzzlehunts
In a puzzlehunt, puzzles generally have no instructions whatsoever, and it is your job to figure out what you even have to do. In addition, it may require outside research. This is in stark contrast from logic puzzles, which give you all the instructions you need, so that your task is just the grid you're looking at.
That said, some hunt puzzles are primarily logic-based, appearing as a set of logic puzzles. Generally they will still require some sort of "aha", something you have to figure out instead of being provided to you. But most of the time, this aha is just an insight you can get in the puzzle without too much outside research. And generally the aha is singular; once you have it, the rest is basically solving normal logic puzzles, perhaps with a twist.
BM Puzzle Competitions
Published and , offline contest
Technically, these were the first ever puzzle events I've ever written. But they were written as a highly informal thing, aimed for a few classmates back in high school that were interested to try these. ("BM" is an abbreviation of my school's name, "Bintang Mulia".)
There were two contests, with heavy emphasis on Sudoku simply because that was the most recognizable puzzle genre.
Fancy Fillomino February
Published , a series on my blog
In February 2013, I decided to post a Fillomino puzzle every day for the 28 days. As the name "Fancy" suggests, each one is a different Fillomino variant. (Well, the first one was a vanilla.) The puzzles were pretty small, mostly 7×7, and they varied in quality. But it was perhaps the first time I put myself on a schedule. I'm pretty sure I was ahead in construction by a few days, although I don't remember by how much.
This list is incomplete and the links don't work. I haven't added the puzzles to the archive.
[2013-02] Fancy Fillomino February
Deception (LMI contest)
Published , contest on Logic Masters India
This was the first contest I've released to the public. (BMPC was earlier, but it's only for very few people in my class.)
It's themed after... well, being deceptive. "Falsehood" has liar clues; "Ambiguity" has clues that are ambiguous or unclear; "Annexation" has genres getting a particular twist. Each section has three genres, and each genre has two puzzles (an easy and a hard one), for a total of 18 puzzles.
I learned a lot of lessons from hosting this contest. What kind of puzzles were appropriate for a contest? How to write clear, concise rules? How to template and put together booklets? (Puzzles being printed too small was a common complaint.) But most importantly, I felt excited to be able to present my own work, and that was the main driving force behind me continuing to write puzzles.
Besides the contest, I believe I also left a legacy for LMI contests in general. Instant Grading was a pretty recent invention in LMI at this point: you would be able to submit your answer for any particular puzzle and have it immediately graded, and you would be able to fix it if it's wrong. Obviously submitting a wrong answer would be penalized, but the penalty hadn't been standardized. For this contest, I used the following method: after 1, 2, 3, 4 mistakes on a puzzle, your potential score for it dropped to 90%, 70%, 40%, 0% respectively. In other words, the penalties for a mistake on the same puzzle were −10%, −20%, −30%, −40% in order, which looked pretty. This has since been a staple and is used regularly on LMI, including LMI's regular Sudoku Mahabrahat and Puzzle Ramayan.
[2013-05] Deception
- Slitherlink (Liar)
- Slitherlink (Liar)
- Masyu (Semi-Liar)
- Masyu (Semi-Liar)
- Smullyanic Dynasty
- Smullyanic Dynasty
- Fillomino (Cipher)
- Fillomino (Cipher)
- Tapa (Elimination)
- Tapa (Elimination)
- Surveyors Heyawake
- Surveyors Heyawake
- Yajilin (Battleships)
- Yajilin (Battleships)
- Nurikabe (Domino)
- Nurikabe (Domino)
- Skyscrapers (Kropki)
- Skyscrapers (Kropki)
First April Sprint Test (FAST) (LMI contest)
Published , contest on Logic Masters India
This test ran exclusively on 01–02 April 2014.
In case the name didn't give it away, it's meant to be an April Fools joke. Every single puzzles was tiny. Most of the puzzles had grids of 6 or fewer cells. The largest puzzle was a 5×5 Nurikabe, followed by a 4×4 Star Battle, then a 3×3 Tapa.
That said, as an April Fools joke, people didn't know about this. We didn't say anything about how the test would look like, so people could be delightfully surprised. We didn't even announce that it was me writing the test. Most people took it well; unfortunately, some people felt bad about it, and we probably could have sent the message better.
One funny thing about this contest was its scoring system. If you finished early, you got a time multiplier equal to 60 minutes (the test duration) divided by the time you took to finish the test. So if you finished in 50 minutes, you would get a multiplier of 60/50 = 1.2 to your final score. Because all the puzzles in this set were trivial, these time bonuses were insane; the fastest solver finished in 2 minutes for a multiplier of 30. It was (and is still) hilarious seeing a top score of 38,510.9 on a 1,273-point contest.
Because all the puzzles are trivial, I'm not putting them to this archive. You can look through the set in the above link to gaze at its beauty.
Polyglot (MIT Mystery Hunt 2015)
Published , hunt puzzle
My first ever hunt puzzle was part of the biggest hunt of the year. Being mostly a logic person, it is logic-related, although it has some aha to discover.
This puzzle isn't very good by my modern standards, but it was a valuable experience to try writing a hunt puzzle.
Hint to start the hunt puzzle
"Polyglot" means someone that speaks multiple languages. All the genres use black/white circles as clues, and all the grids have black/white circles only. What languages do each grid speak? Remember the convention that logic puzzles are supposed to have a unique solution.
Thoughts about the hunt puzzle
The puzzle is about trying every grid with every ruleset. The idea is cute, but it ends up becoming heavy busywork.
One particular problem is that I'm looking for puzzle/ruleset pairs that have a unique solution — very natural for a logic puzzle solver, but this is not quite inspired and some people might just look into any solution.
I believe one reason I wanted to keep this was because some grids ended up being (uniquely) solvable in multiple rulesets, thus explaining the name "Polyglot". But that's a very weak theme, and the puzzle (both the individual grids and the entire hunt puzzle) suffers as a whole.
It should have been tightened up. What the execution should be, I'm not yet sure, but there are ideas I can come up with. Drop the polyglot part, make it a matchmaker. Embrace the polyglot part, every grid is solvable under two rulesets and that makes up chains and all that. Or something else, one way or another.
SPOILER WARNING. Even looking at the list of puzzles will be a spoiler for the hunt puzzle. If you want to try the hunt puzzle as is, don't look here.
Click to reveal
Other than Heteromino below, the two-digit number XY indicates Grid X can be solved under Ruleset Y.
[2015-01] Polyglot
NEW, HUGE, AND CHALLENGING! (LMI contest)
Published , contest on Logic Masters India
Yes, that's the actual title of the contest.
In 2016, I was asked to contribute for Puzzle Marathon 2016. I finally put down the genre that had been in my mind at that time, and brought an entirely new genre with a giant puzzle for it. And then testsolving feedback came, saying it was too difficult.
For reference, although it is a marathon, where every puzzle is significantly larger, it's expected that the puzzle still takes like 30–45 minutes. I believe the testsolver for this one needed 1.5 hours. Unfortunately, that meant my puzzle couldn't go into the Marathon.
But! LMI decided to organize a special "fun contest" for my puzzle. It wouldn't be rated and wouldn't have a time limit; solvers were free to start any time and had until the end of the contest period to submit an answer.
I'm happy the puzzle found another purpose, and that people could enjoy it. You can, too, straight from my archive.
[2016-03] NEW, HUGE, AND CHALLENGING!
Puzzle Marathon 2016 (LMI contest)
Published , contest on Logic Masters India
I was asked to contribute for this event. Unlike regular puzzle contests, solvers would begin each puzzle individually and in any order. They would have an hour to submit the answer for the puzzle. The puzzles themselves were very large, each one easily filling a page.
I sent in a puzzle, which was deemed to challenging. So it became its own contest: NEW, HUGE, AND CHALLENGING!. I sent another puzzle, this time with a different approach, and it tested properly and could be part of the event. So it did.
[2016-04] Puzzle Marathon 2016
The Great Abacus
Published , private set
Puzzlers Club has a regular event called Secret Solver. Similar to Secret Santa, each participant is assigned a recipient; however, instead of buying gifts, they are supposed to write a personalized puzzle for the recipient.
2017 was the first year we did this, and I was assigned TheGreatEscaper. Which is not an entirely unknown name: he is the creator of the genre Haisu, and he has written some incredible puzzles including The Ludicrous Loop and Witless.
A few weeks before the event, TGE suggested the idea of a variant he called "abacus". On a grid logic puzzle, there would be several "abacus lines". Each line had to have the same contents, although skipping empty cells (kind of how Nonogram puzzles treat any amount of empty cells as one). The idea was left broadly open; whether the line would contain shaded cells in a shading genre, or loop segments in a loop genre, or numbers in a number placement genre, or anything else, was up to whoever constructed them.
So I decided to try my hand at it. I focused on shaded cells; all abacus lines in a puzzle must have the same Nonogram-style clue. I chose three genres, representing the letters T, G, E. Each genre had a vanilla puzzle (only with the abacus variant) and a variant puzzle (some other variant, plus abacus). The abacus lines were shaped like the letters T, G, E too, and they were at the exact same locations on all the grids.
Strictly speaking, we only needed to write a single puzzle, but I found writing a set was more cohesive for the theme.
I would later revisit the abacus idea in my birthday LMI contest in 2020, although with a slightly different execution.
General rules about the abacus variant
Abacus rules: There are abacus lines on the grid. For each abacus line, look at the lengths of segments of black cells encountered along the line. (Any positive amount of white cells separate consecutive black segments. This is reminiscent of Nonogram clues.) All abacus lines on the puzzle must read exactly the same way. It's up to you to decide where to start reading each abacus line.
A line might cover a cell multiple times. The line will count the cell every time it enters the cell.
⚠ Prototype warning: These rules were made when I was still trying out how abacus variant would work. As such, the rules are different from how I'm currently using abacus variants. Specifically, in these rules, the start of the abacus is not given to you, and the abacus might reuse cells, making reading somewhat difficult.
Example: In the following example grid, each abacus line reads "1,1,4".
- The T-shaped line, from bottom, has a segment of 1 black cell, then a segment of 1 black cell, then a segment of 4 black cells (the junction is counted twice). This reads 1,1,4. Note that a line can be read from either direction, and it's up to you to determine the correct reading.
- The G-shaped line, from top, has a segment of 1 black cell, then a segment of 1 black cell, then a segment of 4 black cells. This reads 1,1,4. Note that there can be any positive amount of white cells between segments, and any amount (possibly zero) of white cells before the first segment or after the last segment.
- The E-shaped line, from top, has a segment of 1 black cell, then a segment of 1 black cell, then a segment of 4 black cells. (The white cell at the junction separates segments twice.) This reads 1,1,4.
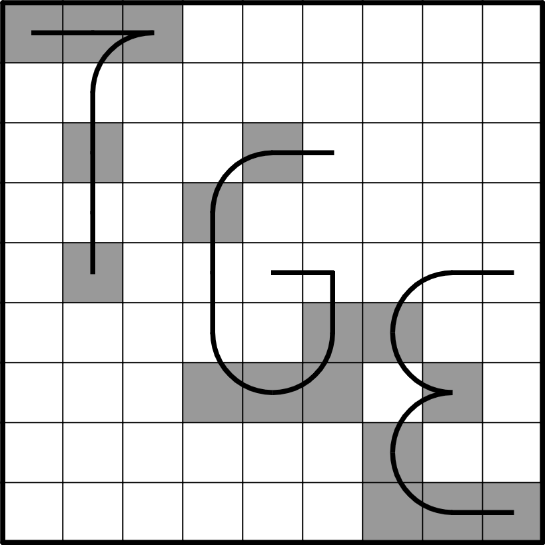
(The image is still PNG because Penpa has some bugs when exporting arcs into SVG.)
Note that all puzzles in this event have exactly the same arrangement of abacus lines as this example. This is so that you can see, from the example, how the doubled-up cells are counted.
[2017-12] The Great Abacus
Unusual and Strange Puzzle Collection (Galactic Puzzle Hunt 2018)
Published , hunt puzzle, co-written with Anderson Wang and with help from Nick Baxter
As part of ✈✈✈ Galactic Trendsetters ✈✈✈, I was invited to write for Galactic Puzzle Hunt, and I decided to go for more hunt puzzle writing.
Naturally, it's more logic puzzle stuff, although the aha is different from my previous hunt puzzle (Polyglot). Also, it turns out to be quite a big, meaty puzzle that took solvers a lot of hours.
I think the puzzle is great to solve casually. This also taught me to scope my puzzles better.
As explained on the solution page, I wrote all the logic puzzles and Anderson wrote the word searches. That wasn't entirely it, though. Since Anderson was well-versed at hunt puzzles, he helped immensely in guiding the direction of this hunt puzzle. (I could write the logic puzzles, but putting them together into a cohesive hunt puzzle was harder.)
Hint to start the hunt puzzle
The rules for the puzzles are not given. (The genre names definitely remind you of existing genres, but there are variants and other complications in play.)
To find the rules, the title holds the key. (You will have to sign up to a website in order to access the rules.)
[2018-03] Unusual and Strange Puzzle Collection
- Almost Yajilin
- Bombardoku
- Cave (LITS)
- Four Winds (Gapped) presented as Eminent D'OHmain
- Snake (First Seen)
- Geometric Distribution
- Kaku Rogue
- Magic Order
- Route
18th 24-Hour Puzzle Championship
Published , part of 24-Hour Puzzle Championship
This was the first time Puzzlers Club wrote a logic puzzle set; not only for 24HPC, but as a whole. We decided on a theme of the digit 3, because "2 and 4 always get the spotlight". (It being "24"-Hour Puzzle Championship, many authors simply theme their puzzles after 2 and 4.)
We had a total of 33 puzzles, which were quite a lot. Most puzzles weren't themed in any particular way; they simply featured the number 3 somehow. That said, we had a section for vanilla genre followed by some 3-based variant of that genre. (For example, we had a vanilla Skyscrapers, followed by an "All 3" variant of it.) For our first showing of an actual, complete set, I wasn't particularly picky in getting a cohesive theme; I simply accepted most — if not all — puzzles submitted by the authors.
Below is a list of my puzzles. But those are not everything. In addition to these, I actually wrote one more puzzle (#1 in the set, Diverse Threes). But it's an observation-heavy puzzle, which I haven't managed to replicate on Penpa. If I figure out how to do that, I'll put it here.
[2018-05] Round 3: "3"
Allied Occupation
Published , private set
After the Secret Solver event in 2017, where I wrote a set for TheGreatEscaper, Puzzlers Club ran another installment of Secret Solver for 2018. I was assigned to write for betaveros.
Now, you need to know, I'm really not confident in writing hunt puzzles. When signing up for Secret Solver, I marked that I would only be able to write logic puzzles, with writing hunt puzzles marked as a "maybe". But betaveros is a good friend of mine. We talked a lot and had several shared interests. We went to International Mathematical Olympiad together in 2012. I thought, this would be a reasonable exception, and set out to write a mini-hunt.
I ended up with a mini-hunt of 5 puzzles + 1 metapuzzle, titled hunt hunt hunt because I was very dumb at that point. If you're interested in doing the mini-hunt, you can look there.
One of the puzzles is called "Allied Occupation". The puzzle itself only shows a bunch of grids marked "examples" and "puzzles"; you have to figure out what they do. Obviously since it's listed here (or at least a big part of it), it's related to logic puzzles. And if you look at the rest of this page, you might be spoiled by its instructions, leaving just the logic puzzle portion for you to solve.
Just like how I used the abacus variant from last year's set in my birthday LMI contest in 2020, I also used the idea here for that contest too.
Hint to start the hunt puzzle
"Allied Occupation" is a very old name for Fillomino. Alternately, you can notice that all solution grids in the examples are valid Fillomino grids. So each example suggests some Fillomino variant. The problem is, the wrong solutions are also valid Fillomino grids, so there is some additional rule in effect that makes the wrong solutions wrong.
Also, each example is a separate example, cluing a separate additional rule. This wasn't made clear in the puzzle and the confusion wasn't intended.
SPOILER WARNING. Even looking at the list of puzzles will be a spoiler for the hunt puzzle. If you want to try the hunt puzzle as is, don't look here.
Something is Off (Galactic Puzzle Hunt 2019)
Published , hunt puzzle, co-written with Alex Pei and Anderson Wang
After the puzzle for 2018, I once again wrote for Galactic Puzzle Hunt in 2019. I actually wrote two puzzles, but the other is not logic-related at all.
This puzzle, once again, goes to my usual foray of logic puzzles as a hunt puzzle. That said, it is followed by a step involving words, and I'm happy I got plenty of help with that portion. The word part, of course, is completely scrubbed clean for this logic archive; if you want to try the puzzle as is, look at the original puzzle.
Not all the logic puzzles are written by me. Below is a list of my puzzles.
Hint to start the hunt puzzle
These are pretty much your usual logic puzzles, except something is off. Some of these puzzles are clearly not unique. Can you find the solutions anyway?
SPOILER WARNING. Even looking at the list of puzzles will be a spoiler for the hunt puzzle. If you want to try the hunt puzzle as is, don't look here.
Click to reveal
[2019-03] Something is Off
April Arrows
Published , a series on my Twitter
Six years ago, I ran Fancy Fillomino February where I wrote a Fillomino puzzle every day throughout February. I decided to give it another try and wrote an Arrows puzzle every day throughout April. A lot of the early ones are vanilla puzzles on bizarre grids.
Unfortunately, my steam ran out in the middle, and the series was unfinished. I got 12 puzzles in before I called it quits, although I had an extra puzzle that I posted later. (That one is marked as 13th in this list.)
I have since learned — from this one and my other creative endeavors — that I probably can't do a consistent schedule with deadlines; if I want to appear like I have a schedule, I need to write the full thing well in advance.
That said, for the amount of puzzles I managed to churn out, I think they are consistently high quality. A couple of them are misses, but in general I like many of them.
That said, they are also incredibly hard, and I was struggling to re-solve my own puzzles. I decided to include a hint for the break-in on most puzzles. Partially so you can read it to get unstuck, partially so I myself can read it for the same reason.
[2019-04] April Arrows
- [2019-04-AprArr-01] Arrows
- [2019-04-AprArr-02] Arrows
- [2019-04-AprArr-03] Arrows
- [2019-04-AprArr-04] Arrows
- [2019-04-AprArr-05] Arrows
- [2019-04-AprArr-06] Arrows (Weighted)
- [2019-04-AprArr-07] Arrows (Missing)
- [2019-04-AprArr-08] Arrows (Spotlight)
- [2019-04-AprArr-09] Arrows (Nightrider)
- [2019-04-AprArr-10] Arrows (Black Hole)
- [2019-04-AprArr-11] Arrows (Pair Sum)
- [2019-04-AprArr-12] Arrows (Liar)
- [2019-04-AprArr-13] Arrows (Cross)
19th 24-Hour Puzzle Championship
Published , part of 24-Hour Puzzle Championship
This year, I didn't write with Puzzlers Club; I wrote a set with Joseph Howard instead. Puzzlers Club wrote two rounds, led by Sophie. Given that I and Joseph are part of Puzzlers Club, I suppose you can say PC wrote 3 rounds. But ours were distinctly different from PC's.
Our set (mine and Joseph's) was themed after the seven deadly sins, with 3 puzzles themed for each of the 7 sins for a total of 21 puzzles. In general, the reception to our set was positive. We forgot to include puzzle points on the puzzle booklet, and one of the puzzles was slightly broken (there was an alternate solution because we didn't specify numbers on the grid were integers), but overall it was a great set.
What about PC, you ask? PC's rounds were themed after Minor Arcana and Major Arcana (more commonly known as simply Tarot cards). They were beautiful constructions.
The main problem with PC's rounds is the scope. The Minor Arcana set had puzzles in common genres, but there were 56 of them, the same number as the number of cards in a deck. The Major Arcana set had 22 fiendishly difficult puzzles in completely foreign genres. Competitors complained about both sets. The puzzles were great by themselves — I do recommend you check them out and solve them leisurely! But as competition sets, they are too long and hard. I took over and led again for the next set.
Below is a list of my puzzles (from the seven sins set). I just realized that the author of each puzzle isn't listed anywhere in the booklets, so this is the first time you'll see who wrote which ones. The ones that aren't here were written by Joseph.
[2019-04] Round 7: "Seven Deadly Sins"
- Doppelblock, presented as Sum Sandwich
- Nurikabe (Lovers)
- Anglers, presented as Allure
- Greener Grasses
- Full Queen, presented as Rampage
We are Puzzlers Club (LMI links: Part 1, Part 2)
Published and , contest on Logic Masters India
After writing our first logic puzzle set (24HPC in 2018), Puzzlers Club was looking to write more things, and I suggested a cheeky idea: each interested author could write a few puzzles independently as a small section, and I would combine the sections together into a set. This way, we would present the various kinds of people in Puzzlers Club.
We got enough interested authors that we decided to make two parts. My section was in Part 1, although I organized both.
While writing, we also made more puzzles than needed, as we tried to figure out how each author could express themself. As a result, we had quite a lot of rejects (PDF file). That said, I didn't have any rejected puzzle. Still, though, if you want more puzzles after doing the contest ones, you can go here.
[2019-07] WAPC 1
Typed Logic (LMI contest)
Published , contest on Logic Masters India
Puzzlers Club decided to write another set, themed after each one of the 18 Pokémon types. (For the Pokémon fans, this was just after The Isle of Armor DLC for Sword and Shield was released. The Stellar type didn't exist yet. As for the ??? type, on retrospect I wish we did something for this, but alas, we just stuck with the "real" types.)
That said, I was busy at this point. I forgot what I was busy for; I might have been finishing up my Masters study, and I might have also been planning for my personal contest a few months later. So, although I organized this contest, I only put in one puzzle.
[2020-07] Typed Logic
- Starry Night, representing
 Fairy
Fairy
25 Years (LMI contest)
Published , contest on Logic Masters India
This was the set that was the most important and dear to me.
I turned 25 years in 2020, and I decided I would summarize my puzzling journey — which was almost 10 years by that point — with a LMI contest. A 25-puzzle contest, containing 12 (+1) genres, each genre taken from one important step of my puzzling life. Most of the genres (and you can even argue all of them) were my inventions, created for various purposes: back when I started publishing puzzles online, made for some event or another, etc. The instructions booklet for the test (download it from the link above) has more exposition about each genre I picked.
The following lists the first 24 puzzles. The 25th puzzle, i.e. the "(+1)", was an English trivia question:
"In what year was I born?"
[2020-11] 25 Years
- Heyawake (Surveyors)
- Heyawake (Surveyors)
- Slitherlink (Tetromino)
- Slitherlink (Tetromino)
- Yajilin (Short)
- Yajilin (Short)
- Linked Signals
- Linked Signals
- Poset Futoshiki
- Poset Futoshiki
- Maximal Archipelago
- Maximal Archipelago
- Kurotto (Abacus)
- Kurotto (Abacus)
- Skyscrapers (All 3)
- Skyscrapers (All 3)
- Fillomino (Mysterious)
- Fillomino (Mysterious)
- Heteromino (Almost Unique)
- Heteromino (Almost Unique)
- Greener Grasses
- Greener Grasses
- Nurikabe (No Touch)
- Nurikabe (No Touch)
Indian Puzzle Championship 2020 (LMI event)
Published , event organized by Logic Masters India
I contributed for the Indian Puzzle Championship this year.
I'll be honest, I have completely no memory of this; I only realized about it when djmathman reminded me that I had these puzzles. Since the Puzzle Booklets seem to be unavailable (they need password but you can no longer get it), I'll reproduce my puzzles here. But since I also forgot about these puzzles, my commentary of them might be not particularly insightful.
Multiple authors contributed to this championship, and our puzzles were scattered over five rounds, so they are also divided into rounds below. Round 1 "Familiar Foes" had genres that appeared in Puzzle Ramayan that year, and Round 2 "Deja Vu" had genres that would belong in some PR round but were cut. Round 3 "Think Different" had more unusual genres. Round 4 "Smart Casuals" had more "casual" genres; this was primarily Tawan's realm. Round 5 "Good Neighbours" was written entirely by Craig Kasper.
[2020-12] Round 1: "Familiar Foes"
[2020-12] Round 2: "Deja Vu"
[2020-12] Round 3: "Think Different"
[2020-12] Round 4: "Smart Casuals"
RED SUS (Silph Puzzle Hunt 2021)
Published , hunt puzzle, co-written with lovemathboy
I was invited to write for Silph Puzzle Hunt, and was asked to help write this puzzle. This puzzle is actually primarily lovemathboy's; I contributed two out of the ten puzzles. I originally only contributed the Fillomino, but when we decided one of the other puzzles wasn't particularly great and we didn't have enough region division puzzles, I wrote the Heteromino as a replacement.
Hint to start the hunt puzzle
"Red sus" is a meme in the video game Among Us. There are hidden impostors among the players, and everyone is suspicious of everyone else. You probably shouldn't trust Red.
[2021-12] RED SUS
20th 24-Hour Puzzle Championship
Published , part of 24-Hour Puzzle Championship
For the 2020 edition of 24HPC, we went for a theme based on "20". We also considered ideas such as "20 Questions", but ultimately we went with the saying "Hindsight is 20/20" and did two rounds themed on this: one for "Hindsight" and one for "20/20".
The first round, "Hindsight", featured two sections. The first section had puzzles based on vision and sight (such as Cave and Kurodoko — although both of those genres appeared only as variants). The second section had genres that were featured in past 24HPC rounds; we picked more unusual genres, because they were less likely to re-appear and so we wanted to give them a second chance.
The second round, "20/20", also featured two sections. The first section featured 20/20 in the puzzle: the clues were the number 20 (or the digits 2 and 0), or the clues were shaped like the number 20. The second section featured 20/20 in the genre: either the genre name was a word repeated twice, or the genre name had the word "double", or the genre had a variant that emphasized doubles or 20.
That's all and good, and we had our two rounds ready well before the submission deadline. And then the COVID-19 pandemic happened.
24HPC was put on hold. We held onto the rounds in the hope that we would get them out sooner or later. Finally, in 2023, we received a message that they were going to hold 24HPC again. We decided our rounds would still be worthwhile to send, and that people would understand. It's unfortunate that we missed the timing, and especially because some people had their puzzles stuck in limbo for three years, but we're glad to finally share them.
[2023-04] Round 10: "Hindsight"
[2023-04] Round 11: "20/20"
21st 24-Hour Puzzle Championship
Published , part of 24-Hour Puzzle Championship
The year of 2024 is special. Many 24HPC authors like the number 24 as a standard go-to theme, and the year being 2024 makes it extra special. (Had the pandemic not happened, this would have also been the 24th 24HPC, which would be insane. It's okay, just means this theme can happen again in 2027.) While we decided to shy away from this overused theme in 2018, this time the theme is strong enough that we'll simply embrace it.
So, Puzzlers Club, once again led by me, wrote two sets of 24 puzzles each. We picked sets of things that naturally had 24. One of them was the Greek alphabet; there are 24 letters in the Greek alphabet. For the other, we realized there were two well-known zodiacs — Chinese (animals) and astrological (constellations) — and each set had 12 things, for a total of 24. We used them as our themes. To differentiate the two sets, one set (the zodiacs) featured the theme primarily in the genre selection; the other (the Greek alphabet) featured the theme primarily on the grid.
Before writing began, I polled people that were interested in writing. We ended up with a total of 32 authors. That's actually a lot, and I was flustered at managing such a large number of people. I ended up splitting the authors into two groups of 16. The first group was writing for 24HPC.
As for the second group, the initial idea was they would write for LMI later that year. But I think I crashed out and lost motivation. I tried to organize a test with a mechanical theme that was too tight, and I think the authors felt too constrained and couldn't express themselves well. Lesson learned: with a large team of authors, don't go for a mechanical theme, at best go for an aesthetic theme. Give leeway for authors of varying experiences to contribute. Later on, I would prioritize their contribution for the 24HPC in 2025.
Anyway, back to 2024. Several people couldn't contribute, for one reason or another, so that we ended up with 11 authors (plus me). I'm wondering how our puzzle turnout would be if I didn't split the authors and let everyone write for 24HPC. But I'm also fine with this decision, so that we can showcase the individual authors better. I wrote 7 puzzles, more than the expected average of 48/12 = 4 puzzles, but I largely did my writing near the end when I picked up leftover themes that others were having trouble with.
I also decided to put in flavor text in the booklets. Some of our thematic connections were quite loose, and being able to explain our decisions would help. It started with why we chose our genres and puzzles, but it also expanded into genre origins, witty quotes, and more. I hope you enjoyed reading through them!
Also, fun fact: I published this section on my website just a few hours after the actual contest finished, although some of this intro text would later be revised months later.
[2024-04] Round 12: "Zodiac"
[2024-04] Round 13: "Greek"
Serbian Puzzle Championship 2024
Published
First off, that year is not wrong. The championship was originally scheduled for 2024, but it was postponed to because of all sorts of difficulties.
I was contacted to contribute puzzles for the championship. They were looking for sets themed after classics, variants, novelties, miniatures, and marathons. After checking, I decided to contribute one full set, for novelties.
What counts as a novelty? Basically whatever genre that people probably have never (or rarely) seen before. I went for the following approach: every single genre was something that already existed before, but usually a modern genre, that was invented in the past couple of years. In addition, I picked genres whose rules are relatively simple to explain. For each of the 8 genres, I wrote 2 puzzles.
I submitted the set in , because they planned for the event the month after. Obviously, that didn't happen for quite a while, so my set was in limbo. But then I noticed that bakpao posted their set, so I poked the organizers and finally received news that the championship took place. Nikola Živanović took first place as expected (mostly because I was unfamiliar with all the other names).
I've also learned that some of my puzzles didn't make it into the set. The second Bunnyhop was "one of the most beautiful puzzles" according to the testers, and became part of the finals, solved on flipboard on stage. On the other hand, the testers thought the second Context had multiple solutions. I have since confirmed this was not the case; it's unique. But there might be translation issues, or the testers might have missed something that would make the alternative solutions invalid.
I'm definitely a bit frustrated about how the championship was run. There's no news about it online anywhere; their website has been inactive for years. This is also why I don't have any link to refer to them. I'm saddened at the communication; if they wrote to me about Bunnyhop and Context, I could check earlier if Context truly had an issue, and I could contribute an additional Bunnyhop puzzle to fill in the set again. But well, it happened. I wrote puzzles, and that's the most important part.
Here are the puzzles, presented as they were meant for the set (i.e. including the second Bunnyhop and the second Context in order). For the ones that appeared in the set, they are accompanied by point values as they appeared in the set. These point values are taken from the results file though, and for puzzles that were not solved by anyone, the entire column was blank and I didn't know their values. So that explains the "???" entries below.
[2025-05] Serbian Puzzle Championship 2024
- Bunnyhop (50 pts)
- Bunnyhop (in finals)
- Contact (20 pts)
- Contact (20 pts)
- Context (25 pts)
- Context (rejected)
- Hit Points (25 pts)
- Hit Points (25 pts)
- Isowatari (25 pts)
- Isowatari (55 pts)
- Simple Gako (??? pts)
- Simple Gako (??? pts)
- Square Jam (20 pts)
- Square Jam (30 pts)
- Turnaround (50 pts)
- Turnaround (??? pts)
22nd 24-Hour Puzzle Championship
Published , part of 24-Hour Puzzle Championship
24HPC has always been hosted in Hungary, but this year is special. Hungary was also the host of World Sudoku & Puzzle Championship 2025. They decided to put the two events together, with 24HPC immediately following WSPC in September. That's why the event didn't run in April–May like usual. I'm not sure if they'll return back to the usual timing next year? We'll see.
In any case, Puzzlers Club as always contributed to the event. However, since 24HPC had much more exposure this year, there were significantly more people — both solvers and writers. Initially, we were given our usual quota of two sets, but I suppose there were more interested authors that they decided to pull one. So we only had one set. So many authors, crammed into a single round.
We noted that 25 is a square number. (And 2025 too!) So on the outset, our theme was "squares and nonsquares". One round would be heavy in squares, from genres like Square Jam to variants like "Shakashaka but all squares" to simply aesthetic themes. The other would be explicitly nonsquares, such as puzzles set on non-square grids, variants such as Shikaku without square regions, and so on. Some genres would appear in both, perhaps with contrasting aesthetic themes or opposing variants. The squares theme was obvious from 25; the nonsquares theme was because we found it amusing to have an explicit anti-theme. (We did one in 2018, when we explicitly themed our round after the number 3, because "2 and 4 kept getting the spotlight".)
After we got cut to one set, we had to think which one would be better kept. I made the call to use the squares set. The nonsquares theme is particularly tough, because the nonexistence of something is a very difficult thing to convey. Pretty much all I can think of requires the "non-square" part to be explicitly called out in the ruleset. That would mean every single puzzle is a variant of sorts. The squares theme is much easier, since it also allows aesthetic themes. That means our less experienced writers can still write vanilla genres with an aesthetic theme, and common genres can also help lessen the load of understanding all the various rules. (Our rounds are notably exotic in nature, with many obscure genres, so having more common genres is always nice.)
At the time we made the cut, we had several puzzles on each theme, around 10–15 each. A few of the nonsquares ones made it into our final set, often paired with a square one (such as Tasquare and Notasquare) for the contrast. What about the other puzzles? We're looking if we want to write more and publish them as a LMI test, or simply let authors post them on their own.
At the time of me writing this, 24HPC has just ended like an hour ago. Our round is in my archive; the rest of the rounds will be added when the puzzles go public, probably. Do try the puzzles, I think they are of very high quality. (And not too difficult, at least pretty reasonable for a contest setting.)
That's all good, but what about me myself? What puzzles did I contribute? Well, turns out I only contributed one, and it's the easiest puzzle in the set. I was busy with academic life.